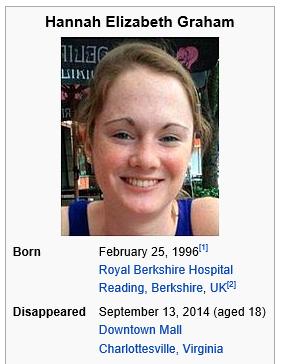RD-blog-number-5145 by Herb Zinser reviews the sequence of murders created by the citizens of the State of California for its violation of hydrocarbon social chemistry laws and the execution of Nature's periodic atomic table undercover agent Caryl Chessman.

Caryl Chessman - Wikipedia, the free encyclopedia
Caryl Whittier Chessman (May 27, 1921 – May 2, 1960) was a convicted robber, kidnapper and rapist who was sentenced to death for a series of crimes ...

Caryl Chessman
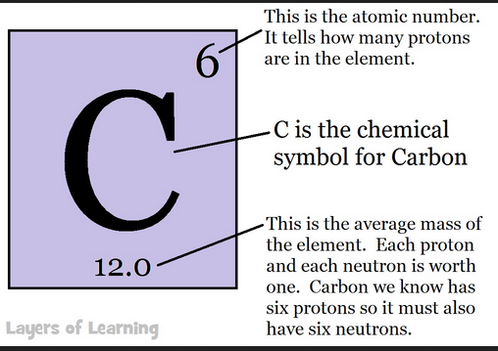
Car. L --> Carbon Languages using chess terminology and SYMBOL MACHINE software technology
On death row - Execution and Nature's systems revenge --> Brookfield Wisconsin
Brookfield hotel was scene of mass shooting in March 2005 ...
Oct 21, 2012 - Brookfield hotel was scene of mass shooting in March 2005.
In 2005, 44-year-old Terry Ratzmann burst into a church service being held by a Church of Living God congregation and fired 22 rounds before shooting himself. He killed seven others in that service.
Ratzmann shot the church’s pastor and the pastor’s family before moving on to others in the conference room at the hotel.
All reports following this shooting indicate Ratzmann acted alone. It also says six of the seven victims were shot in the back and that Ratzmann stopped once to reload.
Terry Michael Ratzmann (1960 – March 12, 2005) was an American murderer who killed seven members of the Living Church of God (LCG) before committing suicide at a Sheraton Hotel in Brookfield, Wisconsin in 2005.
scene of mass shooting in March 2005
scene of mass shooting in March 2005
scene of carbon 12 mass shooting in March 2005
scene of mass shooting in March 2005
scene of mass shooting in March 2005
scene of mass shooting in Jerry March 2005

scene of mass shooting in March 2005
scene of mass shooting in March 2005
Hotel in Brookfield suggests ....
Symbolism | Definition of symbolism by Merriam-Webster
the art or practice of using symbols especially by investing things with a symbolic meaning
or
by expressing the invisible or intangible by means of visible
Below, a hydrocarbon hotel .. information structure
the Living Church of G = universal gravitational constant
the Living Ch ---> Carbon Hydrogen molecules and their living language
scene of mass shooting in March 2005
scene of ...... Jerry March of Dimes
scene of ....... molecule social evolution and the March of Dimensions of string theory and its applications
March of Dimes - Wikipedia, the free encyclopedia
The March of Dimes Foundation is a United States nonprofit organization that works to improve the health of Mother Earth and Mother Nature
scene of mass shooting in March 2005
scene of mass shooting in March 2005
scene of mass shooting in March 2005
Muscular Dystrophy Telethon and Jerry Lewis | Right Turn ...
Sep 5, 2011 - Jerry Lewis, the slap schtick half of the Martin and Lewis team set out ... of the March of dimes than any other in the history of the organization.
Code name --> Jerry Lewis --> Jerry March and Lewis Dot structure



Caryl Chessman and Nature's revenge
Car. L --> Carbon Languages using chess terminology and SYMBOL MACHINE software technology
On death row - Execution and Nature's systems revenge --> Brookfield Wisconsin
On death row - Execution and Nature's systems revenge --> CHar --> Carbon Hydrogen area
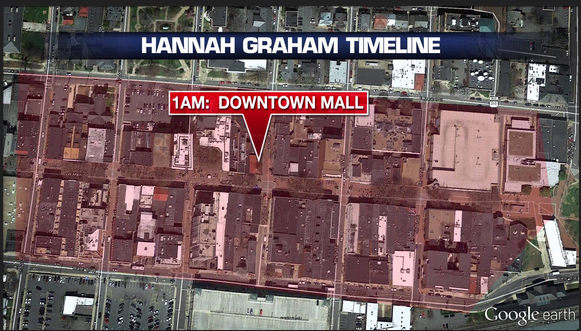
On death row - Execution and Nature's systems revenge --> CHarlottesville wins the lottery
On death row - Execution and Nature's systems revenge --> Hannah Graham .....
selected for her British-American identity
..to send a message to British-American citizens about modern REALITY
and the molecule CH --> Carbon Hydrogen --> CH = CHESS moves of molecules within humans ...... using humans as information display devices
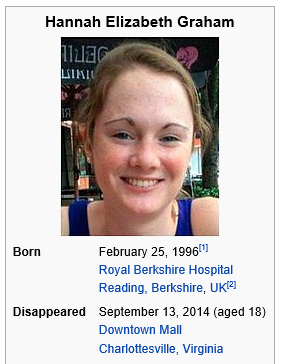
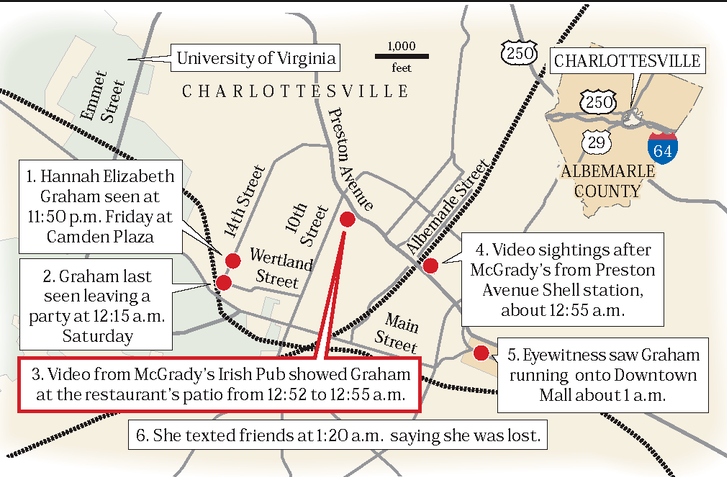
Murder of Hannah Graham - Wikipedia, the free encyclopedia
Hannah Graham (February 25, 1996 – c. September 13, 2014) was an 18-year-
Wanted carbon black agent......

 ...
...
Below, the CH organic chemistry continuum and
the continuum EARTH geography location of
CH = Charlottesville and their social chemistry police department

Let's look at another blog post that provides more ideas for researchers and amateur detectives...
RD-blog-number-5138 by Herb Zinser reviews the tragic signaling EVENTS that occur on Planet EARTH.
Many factors are involved in the creation of these signals by Nature's systems. To help understand some of these tragic signals ... one can percievce the EARTH geography surface as a chessboard with various pieces ...... that are assigned to human represntatives.
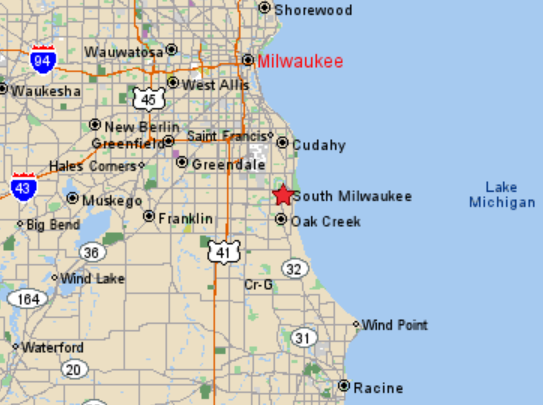
For example, if look at the community of Brookfield ....... west of Milwaukee .....
we see the SYMBOL MACHINE identifier
--> Brookfield --> subset letters --> B + rook + field.
Brookfield hotel was scene of mass shooting in March 2005 ...
-
Oct 21, 2012 - BROOKFIELD — The Sheraton Hotel in Brookfield was the scene of a mass ... Ratzmann shot the church's pastor and the pastor's family before moving ... Male victim seriously injured in shooting near Teutonia & Capitol, wi…WITI
-
Church, Police Probe 7 Murders - CBS News
www.cbsnews.com/news/church-police-probe-7-murders/
Mar 14, 2005 - Gunman Apparently Walked Out Of Church Service Two Weeks Ago. ... opened fire at a church service in Brookfield, Wisconsin on 3-12-05, ... Before the shooting stopped, the pastor, the pastor's son, and five other church ...
Symbolism | Definition of symbolism by Merriam-Webster
the art or practice of using symbols especially by investing things with a symbolic meaning
or
by expressing the invisible or intangible by means of visible
Gunman Apparently Walked Out Of Church Service Two Weeks Ago.
Gunman Apparently Walked Out Of Church Service Two Weeks Ago.
Gunman Apparently Walked Out Of Ch........ Service Two We --> 2 sides BLACK and WHITE pieces.
Gunman Apparently Walked Out Of Chess Service Two Weeks Ago.
stopped, the pastor, the pastor's son
stopped, the pastor, the pastor's son
stopped, the past , the pastor's son
stopped, the past verb tense ... State of Mind .... the past orders son
stopped, the past the pre-sent --> present verb tense
Let's look at another blog post that explains some things ...and includes some refernces to the EARTH geography chess board surface and other version of chess boards ...such as the carbon atom / organic chemistry continuum on EARTH with human life forms embedded as subset entities within Natuire's hydrocarbon continunnu,
Humans are carbon molecule activity and expression entities.
The other blog post ..
The force field death of Hannah Graham
explained by her line integral
Rd-blog-number-5136 by Herb Zinser reviews Nature’s mathematical-physics wars and biochemistry DNA wars for control of EARTH civilizations and their ERRORS and PROBLEMS.
Let’s look at some anaysis of news EVENTS. I repeat another blog post here that lays the information foundation for the math view about Hannah Graham’s tragic death.
University of Virginia fails integration by parts calculus test to save Hannah Graham
Rd-blog-number-5132 by Herb Zinser reviews various DNA bio-math and bio-physics conflicts in the United states and Great Britain.
Let’s look at another post that descibes a situation ..and then we shall look at the University of Virginia (UV) campus system and their DNA math problems and the mathematics death of Hannah Graham ..her final message …… a math curve that she drew while walking in downtown Charolette, NC –> Numerical Control region of North Carolina.
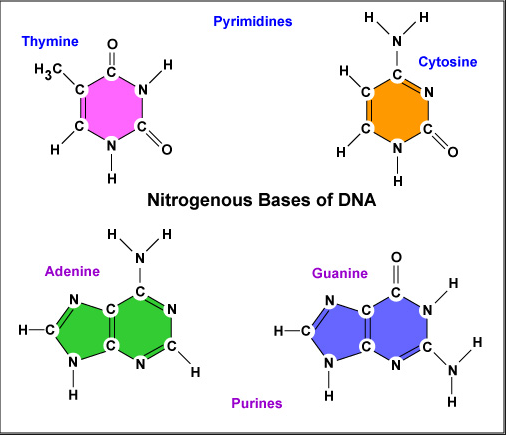
The SiKH (brain) Temple DNA nitrogeous bases wave problems
- Wisconsin Sikh temple shooting – Wikipedia, the free …en.wikipedia.org/wiki/Wisconsin_Sikh_Temple_Shooting
On August 5, 2012, 40-year-old Wade Michael Page fatally shot six people and wounded four others at a Sikh temple in Oak Creek, Wisconsin. Page took his life by …

……………sin wave region of sin wave life forms—> Sikh –> susbet codes
–> Si + KH –> Sin wave K (potassium symbol ) H (hydrogen of water molecule)
about DNA representative Governor Doyle and the nucelotides of Wisconsin sin wave life forms.
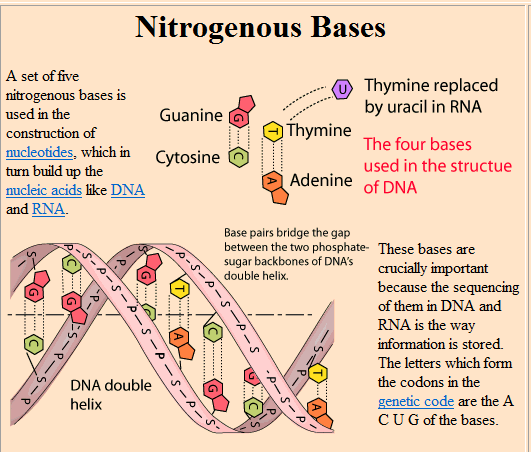
- Deoxyribonucleic acid / DNA | Learn Science at Scitablewww.nature.com/scitable/definition/deoxyribonucleic-acid–DNA-107
Deoxyribonucleic acid (DNA) is a molecule that encodes an organism’s genetic blueprint. In other words, DNA contains all of the information required to build and …
Deoxyribonucleic …….. subset letetrs of the word …|
D.o.y…………le –> 5 symbols of the 16 letters of the word

claiming that DEMOCRATS are electromagnetic (EM) life forms that are superior to the periodic atomic of elements
and its biochemsitry molecules…… molecules that constructed a human structure ….
known as a host platform for the EM life forms to use and abuse.
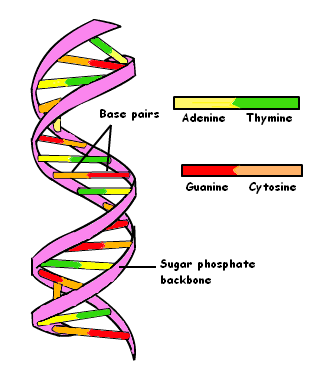
INTERNAL DNA geometry bio-math configuration has
EXTERNAL expression formats to LURE unsuspecting high school graduates into the study of the double-helix twists by going to college and becoming a biochemsitry major.Of course, biochemsitry LURE and SEDUCTION technology has completion …… in the usage of
the multi-purpose female expression system and its concept suggestion.Thus bio-math and calculus(t) curves to guide male student into the study of math fun functions.


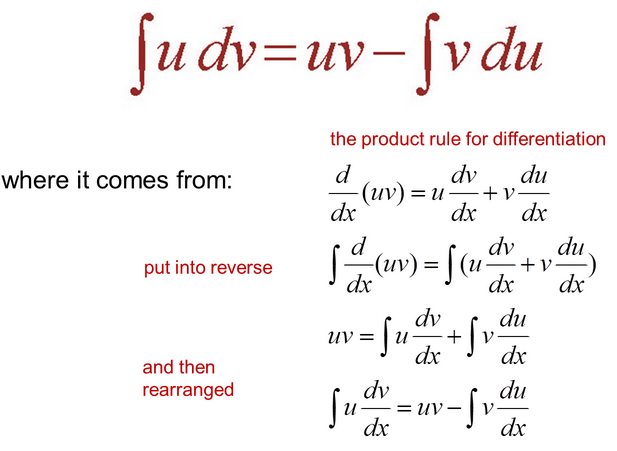

KH with examples ….– > siKH
—> city of Kenosha –> subset letters KH
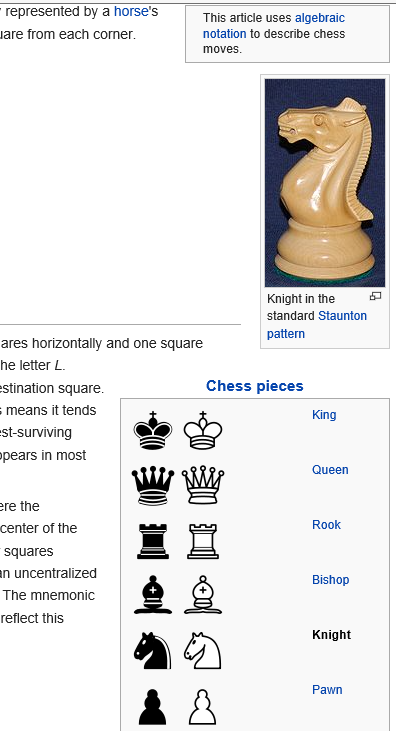
—> KHan –> murder of KH SYMBOL PROCESSOR Haroon KHanSymblos/letets KH …think …think ….spell backwardthink <—mirror word –> Kniht ..explained to Knight
- Knight (chess) – Wikipedia, the free encyclopediaen.wikipedia.org/wiki/Knight_(chess)
- The knight is a piece in the game of chess, representing a knight. It is normally represented by a horse’s head and neck. Each player starts with two knights, which begin on the row closest to the player, one square from each corner.
Knight …sort of the inverse letter sequence of ..the mirror of Think.


near Lake Michigan ( PSSC high school physics and wave tanks and wave mechanics)
skull temple and the brain stem
skull ..em ………………………..em

- Baseball field – Wikipedia, the free encyclopediaen.wikipedia.org/wiki/Base_(baseball)
Second base is the second of four BASE stations on a baseball diamond which must be touched in succession by a base runner in order to score a run for that player’s team.
- Baseball field – Wikipedia, the free encyclopediaen.wikipedia.org/wiki/Base_(baseball)
Second base is the second of four base radio stations on a baseball diamond which must be touched in succession by a DNA base runner who is carrying a secret body language message in order to score a run for that player’s team (Player —> P layers –> Processing layers).

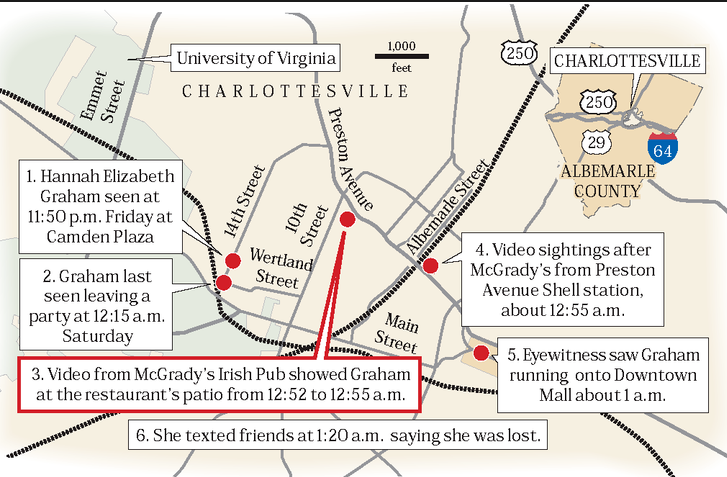
Murder of Hannah Graham – Wikipedia, the free encyclopedia
Hannah Graham (February 25, 1996 ? c. September 13, 2014) was an 18-year-old second-year British American student at the University of Virginia who went …
Her calculus symbol code –> Disappeared: September
Thus …her walking spine ….. a walking calculus symbol.
Line integral – Wikipedia, the free encyclopedia
The terms path integral, curve integral, and curvilinear integral are also used; … In qualitative terms, a line integral in vector calculus can be thought of as a …
Below, she is tracing out path integral …..
Pauls Online Notes : Calculus III – Line Integrals – Part I
-
Lamar University
Vector Fields, Calculus III – Notes, Line Integrals – Part II …. Let’s first see what happens to the line integral if we change the path between these two points.
-
Pauls Online Notes : Calculus III – Line Integrals of Vector …
tutorial.math.lamar.edu/…/LineIntegralsVectorFields.as…
The path integral:
calculating the future from
an unknown past
A fun problem for you, and a matter of life and death for an ant
A (female) soldier ant is returning home from a raid on an enemy colony about 1 meter away from her own anthill. This ant, like the majority of members of many ant species, is completely blind, so finding her way home has been something of an ordeal. An even bigger danger is awaiting her this very moment, however, at the entranceway to her own home. Our soldier ant, during the course of her surprisingly violent battling, has been drenched in the pheremones of her enemy victims. If these pheremones have not worn off by now, then the sentries guarding the entranceway (who are also blind) will mistake her for an enemy. And ants are not known for their patience with enemies.
The question of ?will our soldier be mistakenly killed by her own kind? depends at this moment very critically on how long it took her to walk home. The longer her path was, the better the chance that the smell of her enemies has dissipated, and the better are her odds of surviving her encounter with the sentries. If she walked at a constant speed, then we can assume the enemy pheremones dissipate exponentially (as is the case with evaporation/dissipation of chemicals on a surface). Just to make it concrete, I?ll say that her chance of being killed follows the following law:
,
where L is the total length of her trip home, from enemy anthill to her own. This formula implies that if our ant took a very circuitous route home ? say, 20 meters long ? then she has only about a 13% chance of being killed by the sentries. But if she took the most direct route ? L = 1 meter ? then there?s about a 90% chance of her being dismembered on the spot.
If we knew what path she took, we could use Calculus to figure out her path length L and predict what?s going to happen. But we, the observers, are only watching this moment, as the soldier returns home; we have no idea what path she took. Can we still say anything about what?s going to happen to her?
If we want to know her chance of living or dying, we must average over each of these separate paths, plus an infinite number of others.
I?m only going to say here that it?s possible. Usually, there?s no simple generic solution to a path integral. In most cases you either need a computer or a lot of patience to come up with a result. And you need some way of weighting the different paths, i.e. deciding how likely the different paths are. Here I am just going to use a very simple assumption: that the ant doesn?t stray more than 4 meters from the straight line connecting her origin and destination, and that she doesn?t change her direction more often than every 8 centimeters or so. These are completely arbitrary assumptions, but they allow for a finite result.
Line Integrals with Hannah Graham on the EARTH land math surface of Charlottesville.
Consider a two-dimensional function 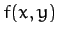 which is defined for all
which is defined for all  and
and 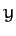 . What is meant by the integral of
. What is meant by the integral of 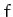 along a given curve joining the points
along a given curve joining the points 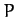 and
and 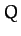 in the
in the  –
–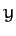 plane?
plane?
Thus we see …… the Carl Jung bio-mathematical-physics collective unconsciousness of the GROUP MIND comprised of the University of Virginia collective …… the student body, professors, employees, and administrators …
that bio-math COLLECTIVE unconsiousness has problems that require conscious thought, lab exercises, and communications to fix.
Now, we have covered some fundamental math application MODELS of the tragedy ..suggested …. by the empirical data generated by Hannah Graham concept.
Let’s advance and consider more.
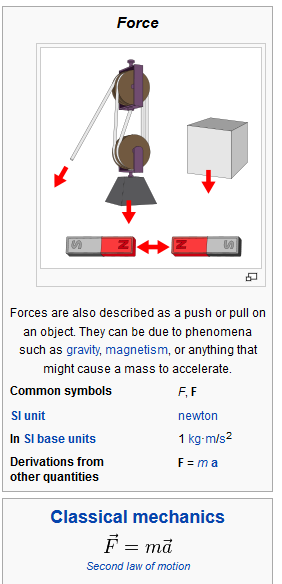
In mechanical physics, in high school ..we do lab experiments … and study the equation
Force = Mass X acceleration
Force, Mass, Acceleration | Zona Land Education
Force equals mass times acceleration. This equation is one of the most useful in classical physics. It is a concise statement of Isaac Newton’s Second Law of …
–> map amino acids (nh) + attributes (data field site)
+ atomic number and alpha/numeric (base 16 hex)
+ tangent existential worlds on EARTH
The original form of Newton’s second law states that the net force acting upon an object is equal to the rate at which its momentum changes with time. If the mass of the object is constant, this law implies that the acceleration of an object is directly proportional to the net force acting on the object, is in the direction of the net force, and is inversely proportional to the mass of the object. As a formula, this is expressed as:
where the arrows imply a vector quantity possessing both magnitude and direction.
Related concepts to force include:
thrust, which increases the velocity of an object
….. in other words ….
Related concepts to the INTELLECTUAL forces of Nature’s systems …
include: trust, the city of an object
Line Integral
Dr. Tatyana Stepanova. Office: S-235 Phone: … This limit is called the line integral of the vector field F over the path C and is denoted. Missing equation.
Line Integrals
- In one dimension, a force can be described by a real number F that is positive if the force is pushing from left to right and is negative if the force is pushing from right to left. When an object is moved from x = a to x = b by a force F the amount of work done by the force is
F (b – a).
- In two or three dimensions, a force can be described by a vector whose magnitude is the strength of the force and whose direction is the direction in which the force is pushing — for example, the vector 2 i represents a force whose strength is two units and that is pushing from west to east. If an object moves under the influence of a force, F, and its motion is represented by the vector S as shown in the figure below

then the work done by the force is

It is often useful to think of ordinary integration as “advanced multiplication.” For example, the area of a simple rectangle whose height is H (Hannah) and
whose base goes from x = a to x = b as shown in the figure below
When an object moves from the point x = a to the point x = b under the influence of a force that is not constant and is given by a function f(x), then the work done by the force is given by

and the simple multiplication of our first formula for work is replaced by integration or “advanced multiplication.”
In this module we look at a two-dimensional or three dimensional situation in which the force is not constant — at different points the force may point in different directions and it may have different strengths. The figure below shows an example. Notice the force is always pointing toward the origin in this particular example.

Not only does the force vary from point-to-point but there is another complication — we are interested in an object traveling along a curved path as shown in the movie below.

Because the force varies from one place to another we call it a force field. A force field is represented mathematically by a vector field. We use the notation
F(x, y) = P(x, y) i + Q(x, y) j
to describe a force field in R2 and the notation
F(x, y, z) = P(x, y, z) i + Q(x, y, z) j + R(x, y, z) k
to describe a force field in R3.
Now suppose that C is a curve in R2 or R3 like the curve shown in the figure below. This example is the path followed by the object in the movie above. We are interested in the work done by a force F acting on an object as it travels along a curve C in a particular direction. In the example below the object travels along the curve C from left to right.

Below, the region of the social and economic forces
We estimate this work in the obvious way. First, we approximate the curve C by a polygonal path — a path made up of straight line segements — as shown in the two figures below.


We choose points s0, s1, s2, … sn along the path C and then connect these points as shown in the figure above.
Below, Hannah generated points s0, s1, s2, … sn along the path C in Charlotesville
Then we estimate the work done on the i-th segment of the path by

and the amount of work done on the whole path by

By using a large number of small segments we can obtain a very good estimate for the amount of work done. The exact amount of work done is obtained by taking the limit of these estimates. This limit is called the line integral of the vector field F over the path C and is denoted

In practice we usually describe the curve C by a function

or

and we divide the time interval [a, b] up into n subintervals. by letting

Vector line integral examples – Math Insight
Example of calculating line integrals of vector fields. … compute the work done by the force field on a particle that moves along the curve that is the …
UWM student was kidnapped, killed over car, authorities say
-
Milwaukee Journal Sentinel
Oct 7, 2008 – Haroon Khan drove a silver 2006 Mitsubishi Lancer Evolution, and Travis W. Zoellick wanted one just like it. When Khan put his up for sale, …
-
Woman charged in slaying of UW-Milwaukee student over car
www.jsonline.com › News › Waukesha County
Oct 8, 2008 – According to the complaint, Zoellick killed Khan so he could steal his car. … was obsessed with obtaining a Mitsubishi Lancer Evolution, and on …
Oct 7, 2008 – Haroon Khan drove a silver 2006 Mitsubishi Lancer Evolution –> the prediction of the possiblility of an MIT policeman shooting in year 2013
in the SCIENCE EVOLUTION wars
Jeffrey Fowle reunited with his family in Ohio – CSMonitor.com
Oct 22, 2014 – Jeffrye Fowle was released from captivity in North Korea, six months after he was taken into custody after leaving a Bible at a nightclub.

- Knight (chess) – Wikipedia, the free encyclopediaen.wikipedia.org/wiki/Knight_(chess)
- The knight is a piece in the game of chess, representing a knight. It is normally represented by a horse’s head and neck. Each player starts with two knights, which begin on the row closest to the player, one square from each corner.
Chess 101: How the Pieces Move | Chess Rules | Idiot's ...
Learn all about how chess pieces move and the rules of chess. Improve your ... Left to right, the pieces are king, queen, bishop, knight, rook, pawn. The Pawn.
Learn all about how chess pieces move and the rules of chess.
Learn all about how chess pieces move and the rules of chess.
Learn all about how chess pieces move and the rules of chess.
For Mr. Male chess player (p layer --> Processing layer).....
Learn all about how chess pieces move and the rules of chess.
Learn all about how ches? pieces move and the rules of ches?.
Learn all about how chest pieces move and the rules of chest.
Learn all about how chest pieces move and the rules of chest.

How to Play Chess : How the Knights Move in ... - YouTube
Learn how the knight moves in a game of chess , from a chess master in this free board game....
Chess Basics 1.5 How the Knight Moves and Captures ... at nightime in ... ch + ar = chess board area of Ch + ar = Charlottesville
This basic chess series teaches you how to play chess. Beginning with how the pieces move, special chess ...
Chess Rules for Movement of the Knight
Since obstructions are not a bar to movement (unless there is a friendly piece on the square where the knight would move) the knight's path of movement has ...
Chess Basics
Chess Basics
Chest Basics for adult females
ch + ar = chess board area of Ch + ar = Charlottesville
..................chest ....................................................lotte --> lottery

Paul Morphy - Wikiquote
Paul Charles Morphy (June 22, 1837 – July 10, 1884), "The Pride and Sorrow of Chess", is considered to have been the greatest chess master of his time, an ..
1837 – July 10, 1884), "The Pride and Sorrow of Chess",
1837............................. "The Pride and Sorrow of Chess",
1837 equation of a water molecule structure (atomic mass 18 ) at 37 degrees Celsius body temperature ...and itrs molecule chess MOVES
via proepr noun Paul Morphy.
Paul Morphy project of Nature's molecules continued their evolution of thought expression systems and SYMBOL MACHINES ....with
Morphy --.> M + orph + phy --> M-theory orphan physics .....with messages for Sandy Hook elementary school treason of elementary physics. projects.

Little Orphan Annie - Wikipedia, the free encyclopedia
The plot follows the wide-ranging adventures of Annie, her dog Sandy and her benefactor Oliver "Daddy" Warbucks. Secondary characters include Punjab, the ...
her dog Sandy and her benefactor Oliver "Daddy" Warbucks
her dog Sandy and her benefactor Oliver "Daddy" Warbucks
her dogma philosophy ... Sandy Hook errors and her benefactor Oliver "BagHDaddy" War
---> shooting at Sandy Hook ordered by Nature's SYMBOL MACHINE regarding their communications problems.
Thus we have Paul Morphy project codes and their evolution ..in physics devleopment project agents
Paul --> Paul Dirac
Paul --> Linus Pauling with Charles Schultz comics, President Jimmy Carter for Peanuts and LINUS and the continuum /Blanket signal of LINUS
Paul --> Wolfgang Pauli
Paul Morphy
............orph + an (Atomic Number) gives word --> Orphan annie and its atomic number / alpha-numeric codes
Thus we see that the secrets of EARTH chess area of Charlottesville is related to the execution of Carl / Caryl Chessman in California ...one of Nature's top undercover agents in the CarL = Carbon Langauge continuum ...such as the HC = Hydrocarbon continuum on an EARTH platform region of CH = Carbon Hydrogen city of CH = Charlottesville and its human CHESS pawns
Caryl Chessman - Wikipedia, the free encyclopedia
§7: THE DATA OF ETHICS (1879) by Herbert Spencer
... in correspondence with external coexistences and sequences;
and still more ... said to be the continuous adjustment of internal relations to external relations.